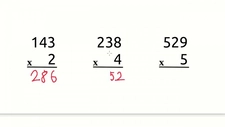
20 Tane 2 Basamaklı Çarpma İşlemiÇarpma işlemi, matematikte en temel işlemlerden biridir ve özellikle iki basamaklı sayılarla yapılan çarpma işlemleri, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine yardımcı olmaktadır. Bu makalede, 20 adet iki basamaklı çarpma işlemi verilecek ve her bir işlemin sonucuyla birlikte açıklamalar sunulacaktır. İki basamaklı sayılar, 10'dan 99'a kadar olan sayıları kapsar ve bu sayılarla yapılan çarpma işlemleri, öğrencilerin sayıların büyüklüğünü kavramalarına, çarpma tablolarını öğrenmelerine ve problem çözme becerilerini geliştirmelerine katkı sağlar. 1. Çarpma İşlemleriAşağıda 20 adet iki basamaklı çarpma işlemi yer almaktadır:
2. Çarpma İşleminin Temel ÖzellikleriÇarpma işlemi, bazı temel özelliklere sahiptir:
Bu özellikler, çarpma işlemlerinin daha iyi anlaşılmasına ve uygulanmasına yardımcı olmaktadır. İki basamaklı çarpma işlemleri, öğrencilerin bu özellikleri keşfetmelerine ve uygulamalarına olanak sağlar. 3. İki Basamaklı Çarpma İşlemleri Uygulamalarıİki basamaklı çarpma işlemlerinin günlük hayatta birçok uygulama alanı vardır. Bu işlemler, özellikle ticaret, mühendislik, bilimsel hesaplamalar ve istatistik gibi alanlarda sıklıkla kullanılmaktadır.
4. Sonuçİki basamaklı çarpma işlemleri, matematiksel becerilerin gelişmesine önemli katkılarda bulunan temel bir konudur. Bu işlemler aracılığıyla öğrenciler, çarpma işleminin özelliklerini öğrenir, problemleri çözme yeteneklerini geliştirir ve matematiğe olan ilgilerini artırırlar. Yukarıda verilen 20 adet çarpma işlemi, bu konunun önemini ve uygulamalarını göstermektedir. Matematik eğitiminde bu tür uygulamaların yer alması, öğrencilerin gelecekteki matematiksel başarılarına olumlu katkılar sağlayacaktır. Ek bilgi olarak, çarpma işlemleriyle ilgili kavramların pekiştirilmesi için çeşitli oyunlar ve etkinlikler düzenlemek, öğrencilerin motivasyonunu artırabilir ve öğrenme süreçlerini destekleyebilir. |
.jpg "Çarpım Tablosu Ezberleme ve Öğrenme Teknikleri")
Bu iki basamaklı çarpma işlemleri gerçekten de matematik eğitiminde oldukça önemli bir yere sahip. Özellikle öğrencilerin sayılarla olan ilişkilerini güçlendirirken, çarpma işleminin temel özelliklerini de keşfetmelerine olanak tanıyor. Verilen işlemler arasında dikkat çeken bazıları var. Örneğin, 12 x 15 = 180 işlemi, çarpma tablosuna aşina olan bir öğrenci için oldukça kolay görünse de, 57 x 62 = 3534 gibi daha karmaşık bir işlem, öğrencinin problem çözme yeteneğini ciddi şekilde geliştirebilir. Ayrıca, çarpma işleminin günlük hayatta nasıl kullanıldığına dair verdiğiniz örnekler, öğrencilerin matematiği daha anlamlı bir şekilde kavramalarına yardımcı olabilir. Bu tür uygulamalar ve oyunlarla zenginleştirilmiş bir öğretim, gerçekten de öğrenme sürecini destekleyecektir. Sizce bu tür matematik çalışmaları, öğrencilerin matematiksel düşünme becerilerini nasıl etkiliyor?
Cevap yazMatematiksel Düşünme Becerileri
Aytunç, matematik eğitiminde iki basamaklı çarpma işlemlerinin önemi gerçekten büyük. Bu tür işlemler, öğrencilerin sayılarla olan ilişkisini güçlendirirken aynı zamanda temel matematik becerilerini de geliştirmelerine yardımcı oluyor. Özellikle karmaşık işlemlerle karşılaşmaları, problem çözme yeteneklerini artırabilir.
Problem Çözme Yeteneği
57 x 62 gibi daha karmaşık bir işlem, öğrencilerin analitik düşünme becerilerini geliştirmelerini sağlar. Bu tür işlemleri çözerken, öğrenciler birçok strateji geliştirmeye ve farklı yöntemler denemeye teşvik edilir. Bu süreç, matematiksel düşünmeyi ve mantıksal akıl yürütmeyi destekler.
Günlük Hayatla Bağlantı
Ayrıca, çarpma işleminin günlük hayatta nasıl kullanıldığına dair örnekler vermek, matematiğin gerçek yaşamla bağlantısını kurmalarına yardımcı olur. Bu, öğrencilerin matematiği daha anlamlı bir şekilde kavramalarına olanak tanır.
Oyunlar ve Uygulamalar
Zenginleştirilmiş öğretim yöntemleri ve oyunlar, öğrenme sürecini eğlenceli hale getirir ve öğrencilerin katılımını artırır. Bu tür uygulamalar, öğrencilerin matematiksel düşünme becerilerini geliştirmelerine ve daha derin bir anlayış kazanmalarına katkıda bulunur. Sonuç olarak, bu tür matematik çalışmaları, öğrencilerin matematiksel düşünme becerilerini olumlu yönde etkiler.