Bu makalede, matematikte önemli bir işlem olan çarpmanın 3 basamaklı sayılarla nasıl gerçekleştirileceği üzerinde durulacaktır. Çarpma işlemi, bir sayının kendisiyle belirli bir sayıda toplanması anlamına gelir ve bu işlem, özellikle büyük sayılarla çalışırken karmaşık hale gelebilir. 3 basamaklı çarpma işlemleri, hem temel matematik becerilerini geliştirmek hem de daha karmaşık matematiksel kavramların anlaşılmasına yardımcı olmak için önemlidir.3 Basamaklı Sayılarla Çarpma İşlemi3 basamaklı sayılar, 100 ile 999 arasında yer alan sayılardır. Bu sayılarla çarpma işlemi yapılırken, genellikle aşağıdaki yöntemler kullanılmaktadır:
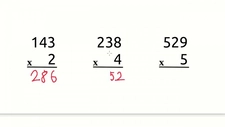
Geleneksel Çarpma YöntemiGeleneksel çarpma yöntemi, her iki sayının basamaklarıyla ayrı ayrı çarpma işlemi yaparak sonuçların toplanmasını içerir. Örnek bir çarpma işlemi üzerinden açıklayalım: Örnek: 234 x 456 1. Öncelikle, 6 ile 234'ü çarparız: 234 x 6 = 14042. Sonra, 5 ile 234'ü çarparız ve bir basamak sola kaydırırız: 234 x 5 = 1170 (1170'ü bir basamak sola kaydırarak 11700 yaparız) 3. Son olarak, 4 ile 234'ü çarparız ve iki basamak sola kaydırırız: 234 x 4 = 936 (936'yı iki basamak sola kaydırarak 93600 yaparız) 4. Şimdi tüm sonuçları toplarız: 1404 + 11700 + 93600 = 106584 Matris YöntemiMatris yöntemi, çarpma işlemini daha görsel bir şekilde yapmamızı sağlar. Her sayının basamakları matris şeklinde düzenlenir ve çarpma işlemi bu matris üzerinde gerçekleştirilir. Örnek: 345 x 678 Burada, 345'in her bir basamağı ile 678'in her bir basamağının çarpımı alınır ve sonuçlar toplanır. Bu yöntem, özellikle büyük sayılarla çalışırken daha az hata yapmayı sağlar. Dağıtma Özelliği Kullanarak ÇarpmaDağıtma özelliği, çarpma işleminin daha kolay yapılmasını sağlayan bir yöntemdir. Bu yöntemde, 3 basamaklı sayılar daha küçük parçalara ayrılır. Örnek: 123 x 456 Bu sayıyı aşağıdaki gibi dağıtabiliriz: 123 x (400 + 50 + 6) Her bir terimi ayrı ayrı çarparak daha basit sonuçlara ulaşabiliriz: 1. 123 x 400 = 492002. 123 x 50 = 61503. 123 x 6 = 738 Sonuçları toplayarak toplamı buluruz: 49200 + 6150 + 738 = 56188 Sonuç3 basamaklı çarpma işlemleri, matematiksel işlemlerin temel taşlarından birini oluşturmaktadır. Farklı yöntemlerin kullanılması, öğrencilere ve matematik meraklılarına esneklik sağlar. Geleneksel yöntemler, görsel yöntemler ve dağıtma özelliği ile yapılan işlemler, çarpma işleminin daha iyi anlaşılmasına yardımcı olur. Bu makalede verilen örnekler, pratik yaparak ve farklı yöntemleri deneyerek çarpma becerilerinizi geliştirmenize katkıda bulunacaktır. Ek BilgilerMatematikte çarpma işlemleri, sadece sayıların çarpımı ile sınırlı kalmaz; aynı zamanda cebirsel ifadelerin çarpımı, matris çarpımı gibi farklı alanlarda da uygulanmaktadır. Bu nedenle, çarpma işlemlerini öğrenmek, daha ileri düzey matematik konularına geçişte önemli bir adımdır. Özellikle, öğrencilerin matematiksel düşünme becerilerini geliştirmeleri için düzenli olarak pratik yapmaları önerilmektedir. |
.jpg "Çarpım Tablosu Ezberleme ve Öğrenme Teknikleri")
.jpg "Çarpım Tablosu Nedir?")
Bu makalede çarpma işleminin 3 basamaklı sayılarla nasıl gerçekleştirileceği üzerine detaylı bilgiler verilmiş. Gerçekten de çarpma, temel matematik becerilerini geliştirmek için kritik bir işlem. Özellikle geleneksel çarpma yöntemi, sayıları basamaklarıyla ayrı ayrı çarparak toplama adımlarını içerdiği için başlangıç seviyesindeki öğrenciler için oldukça öğretici. Ancak matris yöntemi gibi görsel yöntemlerin de kullanılması, özellikle büyük sayılarla çalışırken hata oranını azaltmak açısından avantajlı olabilir. Dağıtma özelliği ile çarpma işleminin daha kolay hale getirilmesi de ilginç bir yaklaşım; bu yöntemi uygulamak, matematikte daha derin bir anlayış kazandırabilir. Bu farklı yöntemleri deneyerek pratik yaptıkça çarpma becerilerini geliştirmek elbette mümkün. Sizce hangi yöntemi kullanmak daha etkili?
Cevap yazMerhaba Mübâreke,
Çarpma işlemi konusunda bahsettiğin farklı yöntemlerin her birinin kendine has avantajları bulunuyor. Geleneksel çarpma yöntemi, özellikle başlangıç seviyesindeki öğrenciler için sayıları anlamada ve temel matematik becerilerini geliştirmede oldukça etkili. Bu yöntem, öğrencilerin sayıları basamaklarıyla ayırıp işlem yapmasını sağladığı için, çarpmanın mantığını kavramalarına yardımcı oluyor.
Görsel Yöntemler ise büyük sayılarla çalışırken hata oranını azaltmak adına son derece yararlı. Matris yöntemi gibi görsel teknikler, işlemleri daha anlaşılır hale getirebilir ve öğrencilerin zihinsel matematik becerilerini geliştirmelerine katkı sağlar. Aynı zamanda, bu yöntemlerin kullanımıyla öğrenciler, sayılar arasındaki ilişkileri daha iyi anlayabilirler.
Dağıtma Özelliği ile çarpma işleminin kolaylaştırılması da etkili bir yaklaşımdır. Bu yöntem, öğrencilerin çarpma işlemini daha soyut bir şekilde kavramalarına olanak tanır ve matematikte daha derin bir anlayış kazandırabilir.
Sonuç olarak, hangi yöntemin daha etkili olduğu, öğrencinin öğrenme tarzına ve seviyesine bağlı olarak değişebilir. Farklı yöntemleri deneyip hangisinin daha iyi sonuç verdiğini görmek, çarpma becerilerini geliştirmek açısından en iyi yol olacaktır. Bu süreçte, pratik yaparak ve farklı teknikleri uygulayarak, öğrencilerin hangi yöntemi daha iyi kavradığını gözlemlemek faydalı olabilir.
Sevgiler,