
Fonksiyonlarda Çarpma İşlemi
Fonksiyonlarda çarpma işlemi, iki veya daha fazla fonksiyonun çarpılarak yeni bir fonksiyon oluşturmasını ifade eder. Bu işlem, matematiksel yapıların derinlemesine anlaşılmasını sağlar ve çeşitli uygulama alanlarında önemli bir yer tutar. Fonksiyonların çarpımının özellikleri, analitik geometri ve kalkülüs gibi konularda da kritik öneme sahiptir.
Fonksiyonlarda Çarpma İşlemi Fonksiyonlar matematikte, belirli bir kural ile tanımlanan ve bir değer kümesinden başka bir değer kümesine elemanları eşleyen yapılar olarak tanımlanır. Fonksiyonlarda çarpma işlemi, iki veya daha fazla fonksiyonun çarpılarak yeni bir fonksiyon oluşturulması anlamına gelir. Bu makalede, fonksiyonlarda çarpma işleminin tanımı, özellikleri ve uygulamaları detaylı bir şekilde ele alınacaktır. Fonksiyonların Tanımı Bir fonksiyon, genellikle f: A → B şeklinde gösterilir, burada A tanım kümesi, B ise değer kümesidir. Fonksiyonlar, belirli bir a ∈ A için f(a) = b şeklinde bir eşleşme sağlar. Fonksiyonlar, birçok matematiksel işlemin temelini oluşturur ve çeşitli alanlarda yaygın olarak kullanılır. Fonksiyonlarda Çarpma İşlemi Fonksiyonlarda çarpma işlemi, iki fonksiyonun çarpımı şeklinde ifade edilir. Eğer f(x) ve g(x) iki fonksiyon ise, bu fonksiyonların çarpımı şu şekilde tanımlanır:
Bu işlem, her iki fonksiyonun değerlerinin çarpımını temsil eder. Fonksiyonların çarpımı, yeni bir fonksiyon oluşturur ve bu yeni fonksiyon f g: A → B şeklinde tanımlanır. Fonksiyonların Çarpımının Özellikleri Fonksiyonların çarpımının bazı temel özellikleri şunlardır:
Bu özellikler, fonksiyonların çarpımı ile ilgili işlemlerin daha kolay ve sistematik bir şekilde yapılmasını sağlar. Fonksiyonlarda Çarpma İşleminin Uygulamaları Fonksiyonlarda çarpma işlemi, birçok matematiksel ve mühendislik problemlerinde önemli bir rol oynar. Bu uygulamalar arasında şunlar yer almaktadır:
Ekstra Bilgiler Fonksiyonlarda çarpma işlemi, analitik geometri ve kalkülüs gibi ileri matematik konularında da önemli bir yer tutmaktadır. Örneğin, iki fonksiyonun çarpımının türevini almak için, ürün kuralı kullanılmaktadır. Ürün kuralı, iki fonksiyonun çarpımının türevini şu şekilde ifade eder:
Bu formül, fonksiyonların çarpımının analizi için son derece önemlidir. Sonuç Sonuç olarak, fonksiyonlarda çarpma işlemi, matematiksel yapıların ve ilişkilerin derinlemesine anlaşılmasını sağlayan önemli bir kavramdır. Fonksiyonların çarpımı, birçok alanda uygulama bulmakta ve matematiksel işlemleri sistematik bir şekilde gerçekleştirmemizi kolaylaştırmaktadır. Fonksiyonların çarpımının özellikleri ve uygulamaları, matematiksel analizin temel taşlarını oluşturmakta ve bu alanın gelişimine katkıda bulunmaktadır. |





.webp)

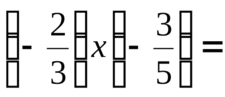



.webp)



Fonksiyonlarda çarpma işlemi üzerine yazdıklarınız oldukça açıklayıcı. Özellikle çarpma işleminin tanımını ve özelliklerini öğrenmek benim için faydalı oldu. Çarpma işleminin analitik geometri ve kalkülüs gibi ileri matematik konularında nasıl yer bulduğunu görmek ilginç. Örneğin, iki fonksiyonun çarpımının türevini almak için ürün kuralını kullanmanın pratikte nasıl bir avantaj sağladığını merak ediyorum. Ayrıca, fiziksel sistemlerin modellemesinde çarpma işleminin nasıl kullanıldığını daha fazla öğrenmek istiyorum. Matematikte bu tür işlemlerle gerçek dünya problemlerini nasıl çözebildiğimiz üzerine daha fazla örnek var mı?
Sayın Yücelay,
Çarpma İşleminin Tanımı ve Özellikleri hakkında yazdıklarımın faydalı olduğunu duymak beni mutlu etti. Çarpma işlemi, matematiksel fonksiyonların temel işlemlerinden biridir ve iki fonksiyonun çarpımı, genellikle iki bağımsız değişkenin etkileşimini ifade eder. Örneğin, f(x) ve g(x) fonksiyonlarının çarpımı (f g)(x) = f(x) g(x) şeklinde tanımlanır. Bu işlem, fonksiyonların birlikte nasıl çalıştığını anlamamız için önemli bir araçtır.
Ürün Kuralı ve Avantajları konusuna gelecek olursak, iki fonksiyonun çarpımının türevini almak için kullanılan ürün kuralı, pratikte büyük bir kolaylık sağlar. Ürün kuralı sayesinde, (f g)'(x) = f'(x) g(x) + f(x) g'(x) formülü ile iki fonksiyonun türevini hızlıca hesaplayabiliyoruz. Bu, özellikle karmaşık fonksiyonlar ile çalışırken önemli bir zaman tasarrufu sağlar ve aynı zamanda hata yapma olasılığını azaltır.
Fiziksel Sistemlerin Modellenmesi açısından çarpma işlemi, birçok fiziksel olayı ifade eder. Örneğin, bir cismin kinetik enerjisi, kütle ve hızın çarpımı ile hesaplanır (KE = 1/2 m v²). Bu tür çarpma işlemleri, fiziksel değişkenler arasındaki ilişkiyi anlamamıza yardımcı olur.
Matematikte, çarpma işlemi ile gerçek dünya problemlerini çözmek adına daha fazla örnek bulmak mümkündür. Örneğin, ekonomide talep ve arz fonksiyonlarının çarpımı, piyasa dengesini analiz etmemizi sağlar. Benzer şekilde, istatistikte olasılık dağılımlarının çarpımı, çeşitli olayların birlikte gerçekleşme olasılığını belirlemekte kullanılır.
Elde edilen bu örnekler ve teorik bilgiler, çarpma işleminin matematik ve fizik alanındaki önemini ortaya koymaktadır. Daha fazla örnek ve uygulama ile bu konulardaki bilginizi derinleştirebilirsiniz.
Saygılarımla,